斜面の原理・・・角ねじの場合の数式解説
前回の斜面の原理(角ねじの場合)では、ねじ締結体(ボルト・ナット)は、リード角βの角度で螺旋状にねじ山が切られている状態であることをご紹介しました。
ねじ締結体においては、締付けトルクTと軸力Fの関係は、ボルトまたはナットのどちらかのねじ山を斜面と見て、他方を荷物と見立てて斜面を荷物を押して進む場合の力の作用からよく説明されます。リード角βは荷物を押して進む場合の斜面の傾斜角と同じになります。
前回は、斜面上で荷物を水平方向に押す力をU、荷物の重さをW、反力をR、摩擦力をM、摩擦角をρ、摩擦係数をμ、傾斜角をβとしました。今回は、前回示した数式の求め方について補足しておきます。
・M:摩擦力とは、斜面上で荷物の移動を妨げる方向に作用する力。
・ρ:摩擦角とは、斜面上の荷物が滑り始める時の角度。
・μ:摩擦係数とは、斜面上に垂直な方向に作用する反力Rと摩擦力Mの比率。(tan ρ = μ = M/Rの関係式)
・β:斜面の傾斜角はリード角とも呼ばれます。JIS用語では、「平行ねじの場合は、ねじ山のつる巻き線と、その上の1点を通るねじの軸に直角な平面とがなす角度」と定義されています。⇒ ねじの構造について
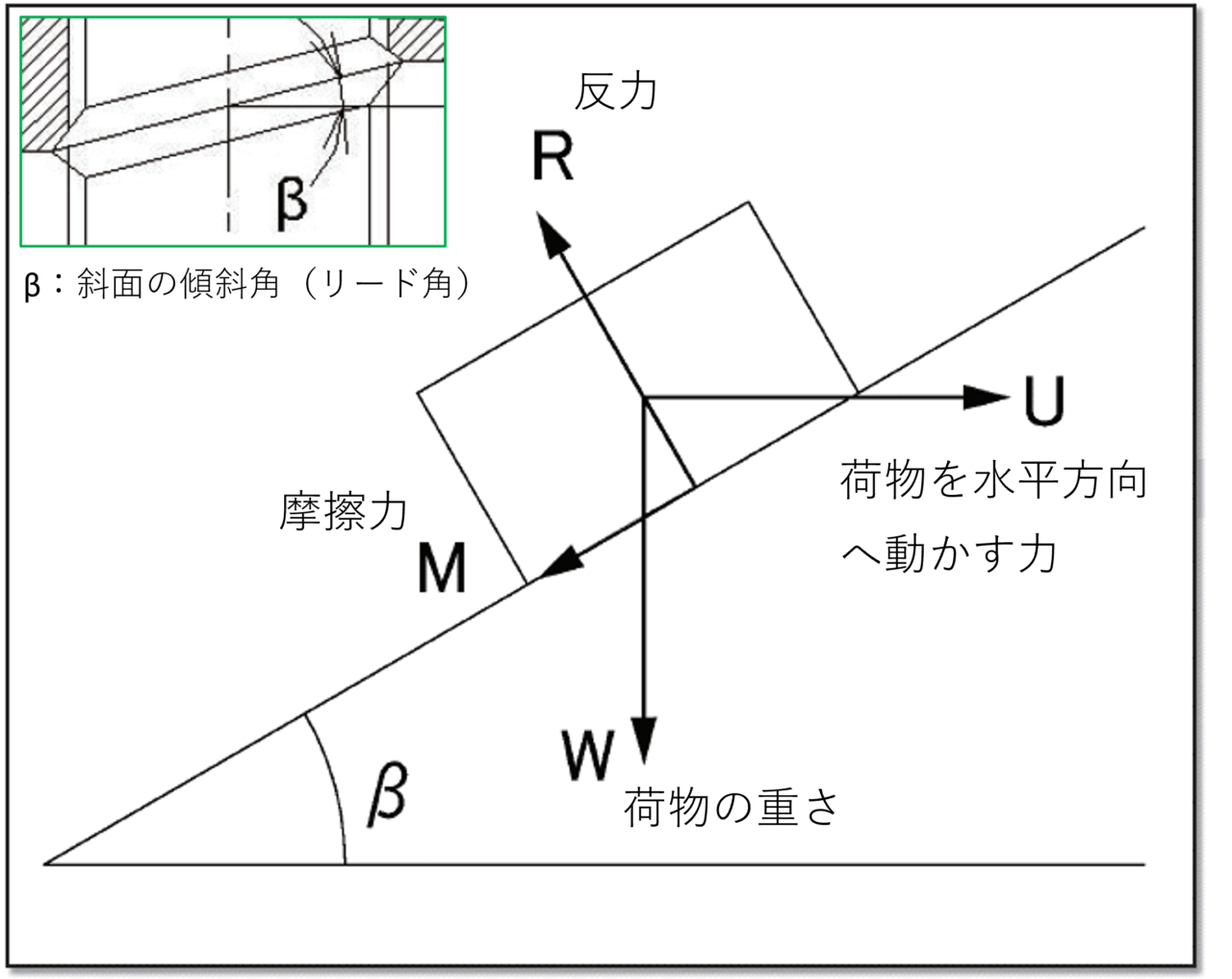
図1.説明図(斜面の原理)
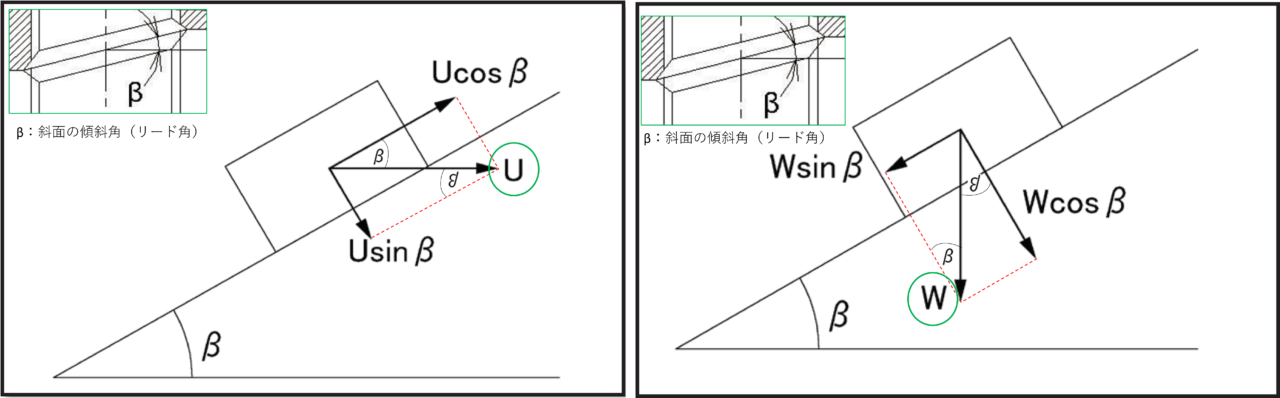
図2.説明図(U:水平方向に押す力の分解) 図3.説明図(W:荷物の重さの分解)
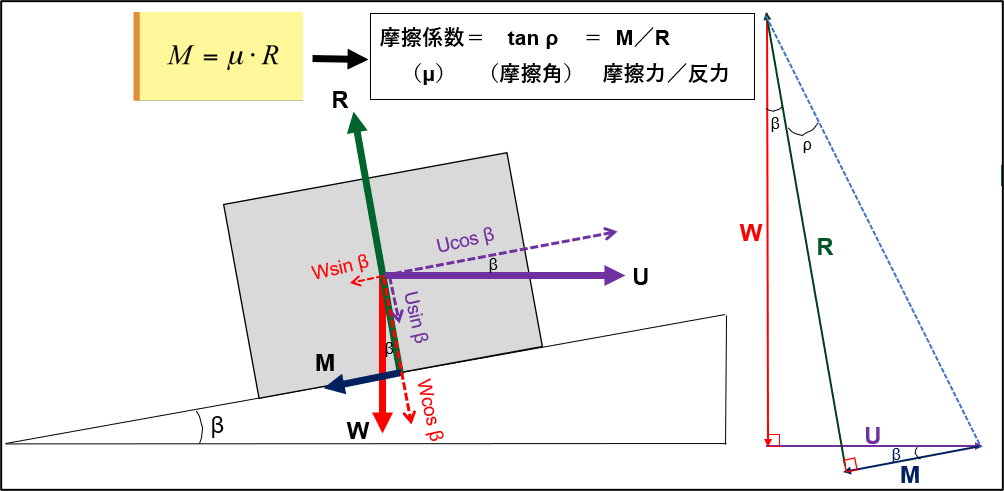
図4.説明図(ベクトルの関係)
前回の斜面の原理では、荷物を押して斜面を上る場合の水平方向に押す力Uを以下の式で求められることを示しました。
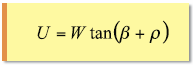
式(1-1)
また、ここで斜面を上る場合の摩擦力Mを以下の式で求めることも示しました。
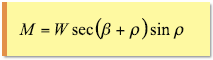
式(1-2)
今回は、この2つの数式を求めていく過程を示します。
◇式(1-1)の場合
この数式を求めるためには、三角関数の知識が必要となります。「sin:サイン、cos:コサイン、tan:タンジェントで聞き覚えがあるものです。」
図1の各々の力関係の中で、図2:水平方向に押す力、図3:荷物の重さ(重力)に分解することから始まります。
図4にて、各々の力の関係を見ていきます。
斜面では、力がつり合っている状態では、
U cos β = W sin β + M 式(1-3) であるので、
M=μR → R = U sin β + W cos β 式(1-4)を代入する。
U cos β = W sin β + μ(U sin β + W cos β) 式(1-5)となります。
U cos β = W sin β + μ U sin β + μ W cos β
U(cos β – μ sin β) = W(sin β + μ cos β) ここで、μ = tan ρ を代入する。
U(cos β – tan ρ sin β) = W(sin β + tan ρ cos β) ここで、sin β = tan β cos β を代入する。
U(cos β – tan ρ tan β cos β) = W(sin β + tan ρ cos β) ここで、両辺を cos β で割る。また、tan β=sin β/cos βより、
U(1 – tan ρ tan β) = W(tan β + tan ρ) ここで、次の加法定理を代入し、
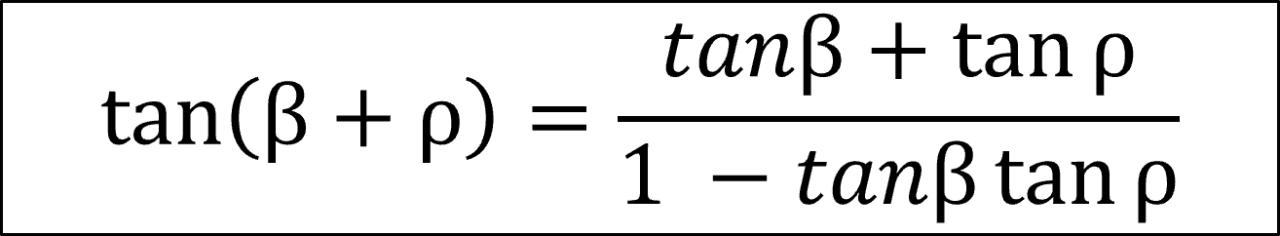
U(1 – tan β tan ρ) = W{ tan (β+ρ) (1 – tan β tan ρ)} 従って、両辺を(1 – tan β tan ρ)で割って、
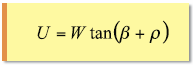
式(1-1) が得られた。
◇式(1-2)の場合
ここでもポイントとなる式は、以下です。

式(1-6)
![]()
式(1-7)は、式(1-6)に式(1-4)を代入して求めます。
![]()
式(1-8)は、式(1-1)を代入して求めます。
ここからは、三角関数の知識を更に活用していきます。
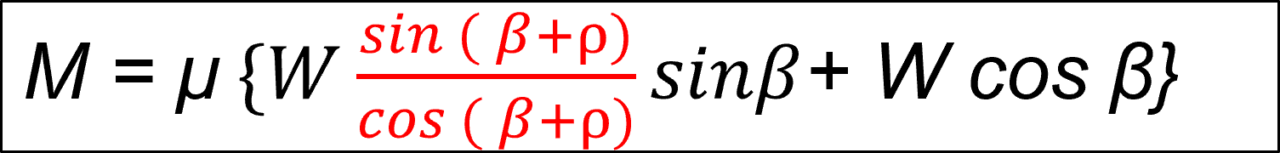
式(1-9)は、tan の置き換えです。
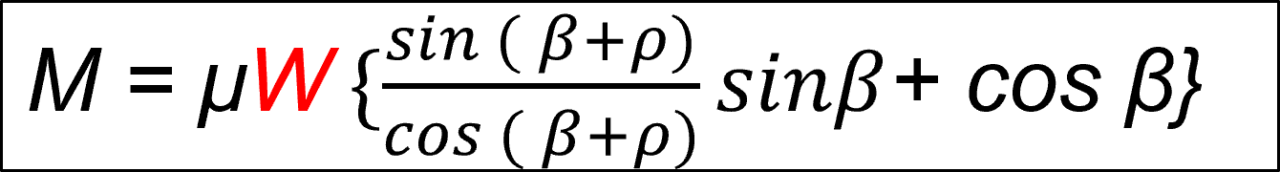
式(1-10)は、Wで括ります。
式(1-11)下式は、加法定理 sin(A±B) = sin A cos B ± cos A sin B、cos(A±B) = cos A cos B ∓ sin A sin B より、
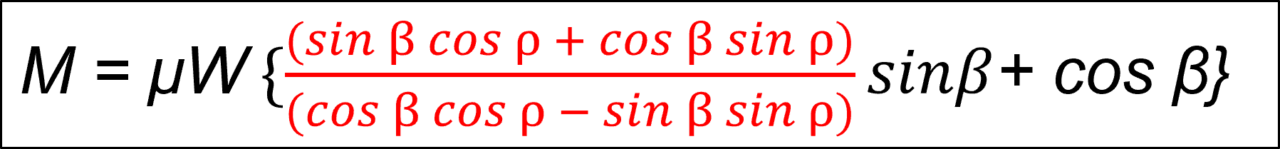
式(1-11)
式(1-12) 下式は、計算式を処理しやすくするために、1になる同じ分数を挿入する。
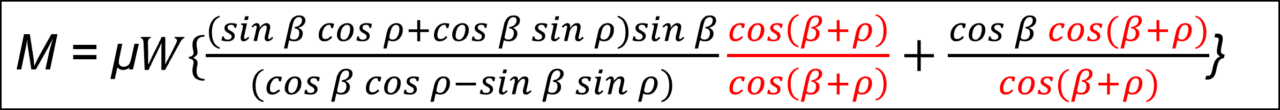
式(1-13) 下式は、cos ( β + ρ )= cos β cos ρ – sin β sin ρ を式(1-12)に代入する。
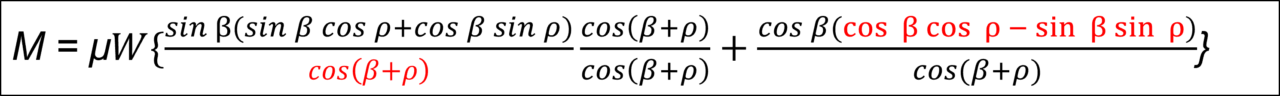
式(1-14)下式は、単に分子と分母の同じものを消去。
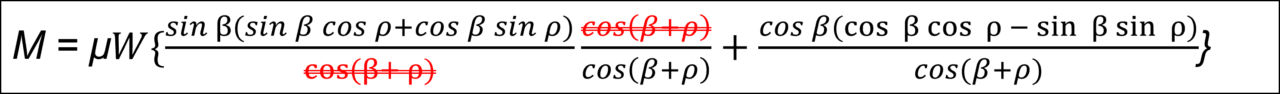
式(1-15)下式は、cos ( β + ρ ) で括る。
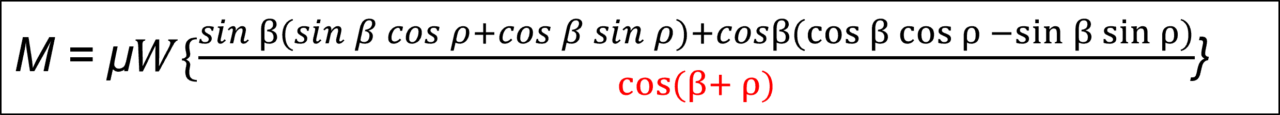
式(1-16)下式は、数式を展開して、sin β cos β sin ρ が消える。

式(1-17) 下式は、cos ρ で括る。
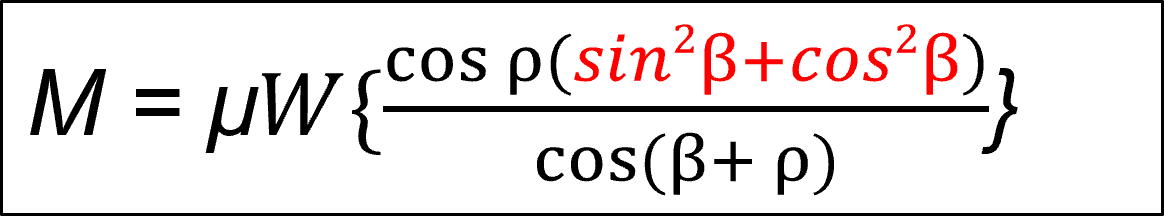
![]()
式(1-18)下式は、μ = tan ρ に変換して、

式(1-19)下式は、tan ρ を変換した後で cos ρ が消える。
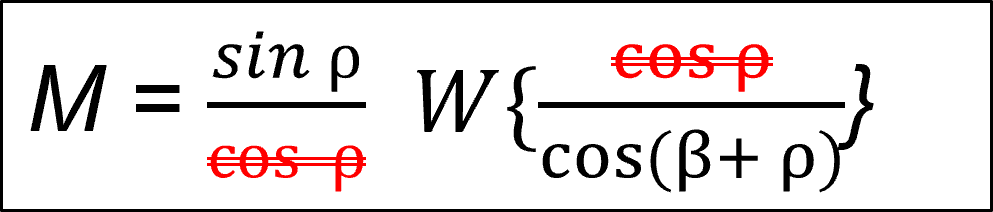
式(1-19)は、三角関数の公式(式-1-20)を使用してcos を sec に変換する。
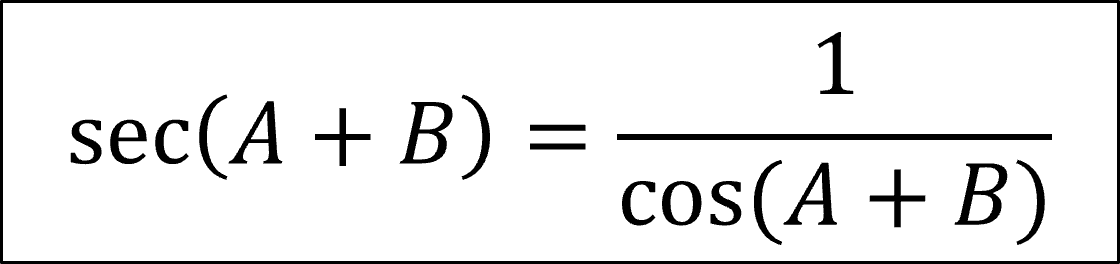
式(1-20)
最終的に、式(1-2)となって摩擦力Mを求めることができる。
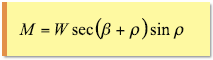
式(1-2)
以下の技術コンテンツもご確認ください。





