ねじ締結体のボルトはどのように設計すればよいのか?
図1に示すような2枚の中空円筒を1本のボルトとナットで締結しているねじ締結体のボルトを例に、設計手法を解説していきます。
ボルト締結体は、初めに初期ボルト締付け力Ffで締め付けた場合を考えます。
この状態で図1に示すように一般的には軸方向に引張荷重Wあるいは軸直角方向にせん断力Qが作用することを想定します。
ここでは、軸方向荷重Wが作用する場合について話を進めます。
そうすると、ボルトは引っ張り力の増加分Ffが追加され、他方2枚の中空円筒(これを被締付け物と呼ぶ)の接合面からはFcの力が減少します。すなわち、ボルト軸力は、Ff+Ftとなり、接合面の締付け力は、Ff-Fcとなります。
力のつり合いから次式(1-1)が与えられます。
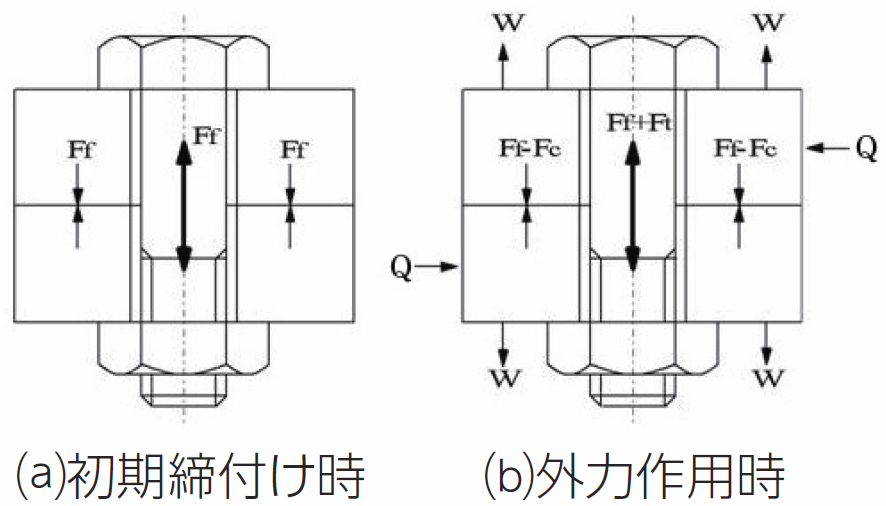
図1.中空円筒を締結したボルト締結体
![]() (1-1)
(1-1)
しかし、FtとFcが未知数で、与えられる方程式は1つしかないため、この問題はこのままでは解けません。いわゆる不静定問題(静力学的つり合い条件だけでは方程式の数が足らずに解けない)に相当します。この解法は歴史的には1938年にドイツで出版された本に初めて示され、今でも日本の設計の本には示されています。
しかし、外力が作用したときにFtの値がいくらになるかを予想することが問題です。
実は長い間この値の求め方が知られていましたが、あまり当てにならない手法が使われていました。詳細は後述します。
ここでFt/Wの値を内力係数と呼び、一般的には次式で表します。
 (1-2)
(1-2)
Φの値が求まれば、式(1-1)より、Fcの値は次式で与えられます。
![]() (1-3)
(1-3)
内力係数Φとは
内力係数Φとは、外力Wが作用した際にねじに生じる軸力の増加分Ft(接合面から失われるFc)を決定する割合のことです。
ここで、このようなボルト締結体(締結体=ボルト・ナットと被締付け物からなる)を設計するにあたって、かつてドイツのJunker氏は以下の1)から3)を考慮することが大事であると指摘しました。
また、本稿では4)として接合面に残留する力(応力)を重視して追加しています。
- 繰り返し荷重(WあるいはQが機械の作動中に何回も繰り返して作用する)に対してボルト(ねじ)が緩まないこと。
- 外荷重(WあるいはQ)の作用に対してボルトに生じる最大の応力がボルト材料の降伏応力を超えないこと(あえてボルトの降伏応力になるように締付ける方法もあるが、ここでは基本で述べることにします)。
- 繰り返し外荷重に対してボルトが疲労破壊しないこと。しかし、これだけでは実際の設計では不足であり、締結体の機能を遂行するための条件が必要であり、以下を加えることにします。
- ボルト締結体の機能を遂行するために必要な接合面応力が確保されている。
上記4つの条件を満たすためにはどのようにボルトを設計するか、すなわち、ボルトの呼び径(径の大きさ)と強度区分(ボルトの強さ)を選択するかが問題と考えます。
さらにボルト初期締付け力Ffを決定し、この値を得るためにボルトとナットを締付けるトルクTが必要となります。
上記1)に対する設計方針
外力の作用に対してゆるみを生じさせないためには、VDI2230(ドイツ技術者協会が発行する高強度ねじ締結の体系的計算法)によると、高強度ボルトに対しては、初期締付け力Ffを締付けによるせん断応力を含めたミーゼスの相当応力がボルトの降伏応力(耐力)の90%以下にできるだけ大きくとることを示しています。
おねじの締付けによって発生するせん断応力τは式(2-1)で表されます。
![]() (2-1)
(2-1)
ここで、
φ:ねじのリード角、ds:有効断面積に等しい円の直径、μ:摩擦係数、d2:おねじ有効径の基準寸法
式(2-1)と初期締付け力(Ff)maxによる応力σfmax(=(Ff)max/As)を用いると、ミーゼス相当応力σvは以下のようになります。
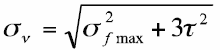 (2-2)
(2-2)
![]() (2-3)
(2-3)
ここで、σvはボルト材の降伏応力、Asは有効断面積です。
さらに、外力が作用したときに、接合面に残留する締付け力Fkerfを指定します。
上記2)に対する設計方針
軸方向外力(荷重)Wが作用すると、ボルトの軸力は最大でFf+Ftとなる。ボルトが破損(降伏応力を超える)するときには、ボルトのねじのナットとのはめあいの座面側第一ねじ谷底の応力が最大になることが知られています。
従って、従来の慣行では上記最大の力をねじの有効断面積で除した値(応力)が降伏応力以下になるようにFfを決定することになります。しかし、ボルトを締付けるときにボルト軸にねじりによるせん断応力が発生するので、この破損応力(降伏応力なしは耐力)を超えないためには、
![]() (2-4)
(2-4)
ここで、Ftの値は式(1-1)から求められます。しかし、実際にはボルトの締付け力はばらつくので、どのようにするかが問題です。
一般的に、ガスケットなどを挿入しない図1に示されるボルト締結体などでは例外(コネクチングロックボルト)を除いて、軸方向外力Wが作用した時のボルト軸力の増加分Ftは0.1W以下です。
上記3)に対する設計方針
疲労でボルトが破壊するのは、理論的にはおねじの座面側第一ねじ谷底です。図1に示すように外力Wが0~Wまで作用すると、ボルト軸力の変動はFf〜Ff+Ftになります。図2はボルト初期締付け力Ffで締結した締結体に外力Wが作用するとボルト軸力がFf+Ftになることを示しています。
Ftは初めWの増加に対して直線的に増加し、やがて接合面が分離を始めると曲線状に増加します。接合面が完全に分離すると、Ft=Wとなり、45°の傾きの直線となります。Ffがより小さいと、外力W0の値に対して、接触面が分離するため、Ftの値は大きくなります。Ffがより大きくなると、同じ大きさのW0が作用していてもFtの値はより小さいことを示しています。
一般的に、ねじの谷底の断面積Arを使うので、ボルト応力の変動は(Ff+Ft)/Ar 〜 Ff/Arで表されます。
そうすると、応力振幅は次式であり、これがボルト材料の疲労限度σα以下にする必要があります。
![]() (2-5)
(2-5)
接触応力σmは、 σm=(Ff+Ft /2)/Ar となります。
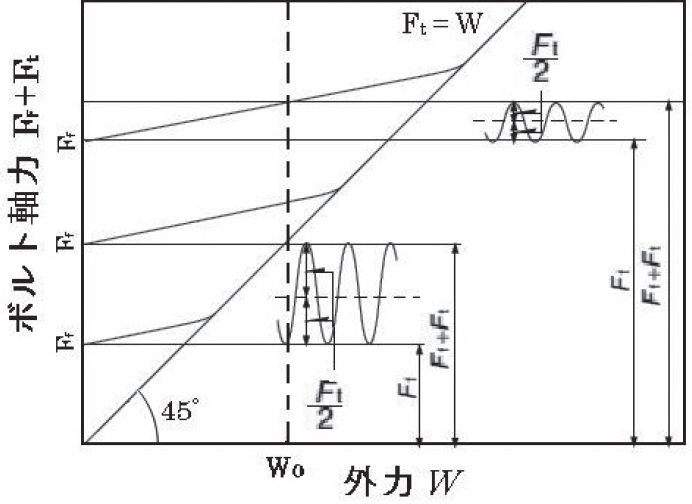
図2.ボルト軸力-外力線図
上記4)に対する設計方針
外力が作用すると被締付け物接合面(接合面の断面積をAiとする)応力は、以下となります。
![]() (2-6)
(2-6)
これが必要な応力σreq以上に確保する必要があります。そうしないと、例えば、ねじり荷重が作用したときに接合面が滑って回転してしまう。回転しないように接合面応力が必要である。さらにガスケットを入れるような密封性(漏れないように)を必要とする場合も同様である。
従って、以下の式を満足する必要があります。
![]() (2-7)
(2-7)
以上の設計の基本方針を述べましたが、結局どうすればいいのでしょうか?
初めに述べたましたように外力Wが作用したときに、ボルトに発生する軸力の増加分Ftと接合面から失われる力Fcを設計段階でより正確に推定する必要があります。
ボルトのばね定数をKt、被締付け物の圧縮ばね定数をKcとするとき、式(1-1)の方程式を満足する条件と、外力Wが作用したときのボルト座面のボルトの伸びと被締付け物の伸びが等しい条件から、FtとFcをばね定数KtとKcを用いて、Thum&Debus は以下の式を提案しました。
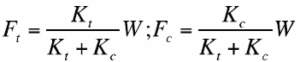 (2-8)
(2-8)
図3は、FtとFcをKtとKcを用いて表した線図を示します。KtとKcの線が交わる点が初期締付け力Ffを示します。なお、横軸はボルトの伸び(Kt)及び被締付け物の縮み(Kc)を示しています。
しかし、ばね定数Kcを如何に求めるかが長い間の問題でした。実験的に座面の見えないところの変位を上手く測れないことが原因であり、推定式が多く提案されています。1960年代になり、Thum&Debus の式を用いて得られた内力係数の値が実験で測定された値とかなり異なることが判明しました。
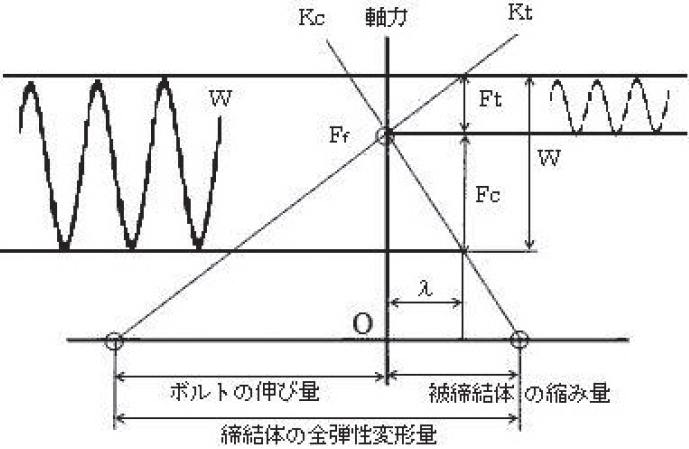
図3.ボルトの締付け線図
内力係数は、安全なねじ締結体を設計する上で非常に重要なものですが、その重要性が十分に認知されていません。そこで、ボルト締結体の設計法を段階的に公開していきますのでご確認をお願いします。
ご参考資料はこちら





