平均応力について
金属疲労では応力が繰返し部材に負荷されます。この繰返し応力を表す条件として、応力振幅と平均応力があります。応力振幅は最大応力と最小応力の差の半分の大きさで、S-N曲線において縦軸に表示されます。一方、平均応力は最大応力と最小応力の和の半分の大きさ、すなわち平均値です。S-N曲線には直接表示されませんが、平均応力は疲労強度・疲労限度の大きさに影響し、引張の平均応力がかかると疲労限度は低下し、圧縮の平均応力がかかると疲労限度は増加します。そして引張の平均応力がより大きい条件下の方が疲労限度は低下する傾向になります。
図1の応力波形は、両振り、片振り、そして部分片振りの状態を示したものです。Y軸の上方向が引張応力側で、波形の波の中心線が平均応力になります。両振りでは平均応力が0であり、片振りでは応力振幅と平均応力が同じ値になります。
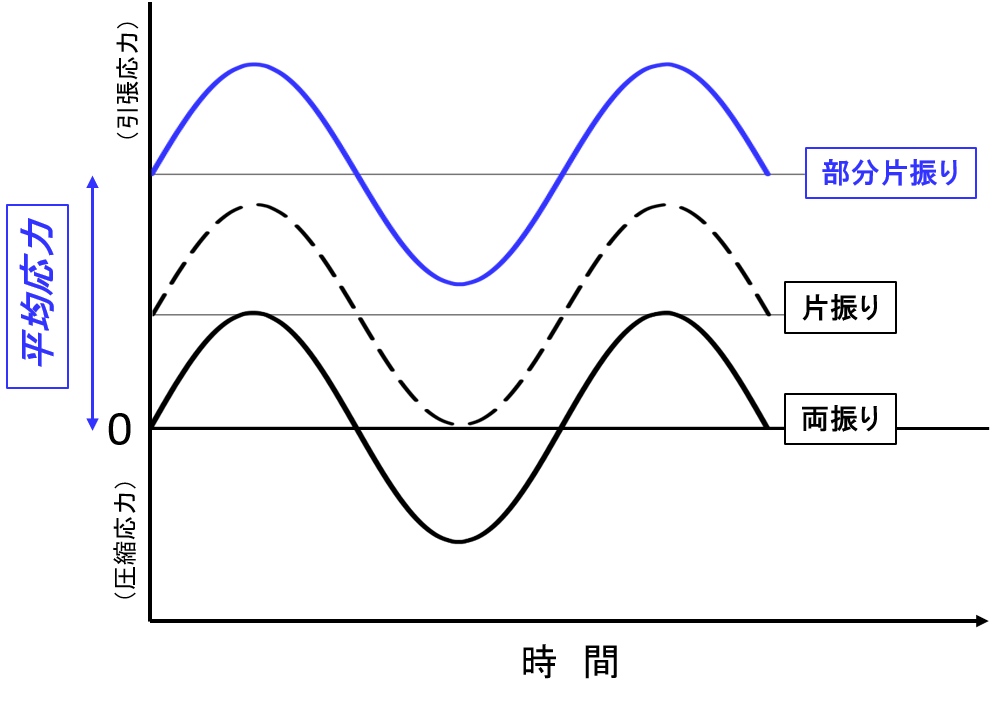
図1 応力波形と平均応力
疲労限度線図
疲労の繰返し応力で引張の平均応力がかかっていると疲労限度は低下します。この低下の度合を示す線図が疲労限度線図と呼ばれるもので、X軸を平均応力の大きさ、Y軸を疲労限度として図示します。X軸の原点は両振りの平均応力0を意味し、X軸の正方向が引張の平均応力、負方向が圧縮の平均応力を意味します。疲労限度線図は通常右下がりの緩やかな曲線になります。疲労設計では疲労限度が重要であることからY軸には一般に疲労限度を取りますが、S-N曲線において疲労限度が出現しない場合や決まった繰返し数でその疲労強度を設計する場合には時間強度を取ることもあります。平均応力が圧縮側になりますと疲労限度は増加します。
X軸上に真破断力をプロットし、Y軸上に両振り(平均応力0)の疲労限度の大きさの点をプロットし、両点を直線で結ぶ線図がσw―σT線図とも呼ばれる疲労限度線図です。一方、X軸上に引張強さをプロットし、Y軸の両振り疲労限度の点と直線で結ぶ線図が修正グッドマン線図と呼ばれます。X軸上の任意の平均応力に対する直線上の交点のY軸値が任意の平均応力に対する疲労限度を示します。設計において材料の引張強さは必ず把握すること、また安全側に位置することから、一般的に修正グッドマン線図を用いて任意の平均応力のもとでの疲労限度を求めることが多いです。
疲労限度線図においてX軸とY軸に降伏応力の点を取って直線で結びますと、その外側領域では最大応力が降伏応力を超えることになります。図2のグレーで示した領域は疲労による繰返し応力の最大応力が降伏応力を超えない安定域を示すことになります。
実機の機械部品では機械加工、表面処理、溶接、熱処理などの工程によって多くの場合に残留応力が発生します。材料の応力がかかる部位に残留応力が存在する場合は、その残留応力値を加えた平均応力値として同様に疲労限度線図で疲労限度を補正することになります。但し、引張の残留応力ではプラス側に数値を取りますが、圧縮の残留応力ではマイナス側に直線を延長してマイナス側の数値で読み取ります。すなわち、ショットピーニングのように部材表面に圧縮の残留応力を発生する場合には疲労限度を増加させる働きがあります。また、残留応力は疲労の進行とともに減少する場合があります。このため対象部位の初期残留応力を求めて疲労限度線図で補正してもずれることになりますが、引張側の残留応力の場合は残留応力の減少とともに疲労がより安全側に移行しているとも言えます。
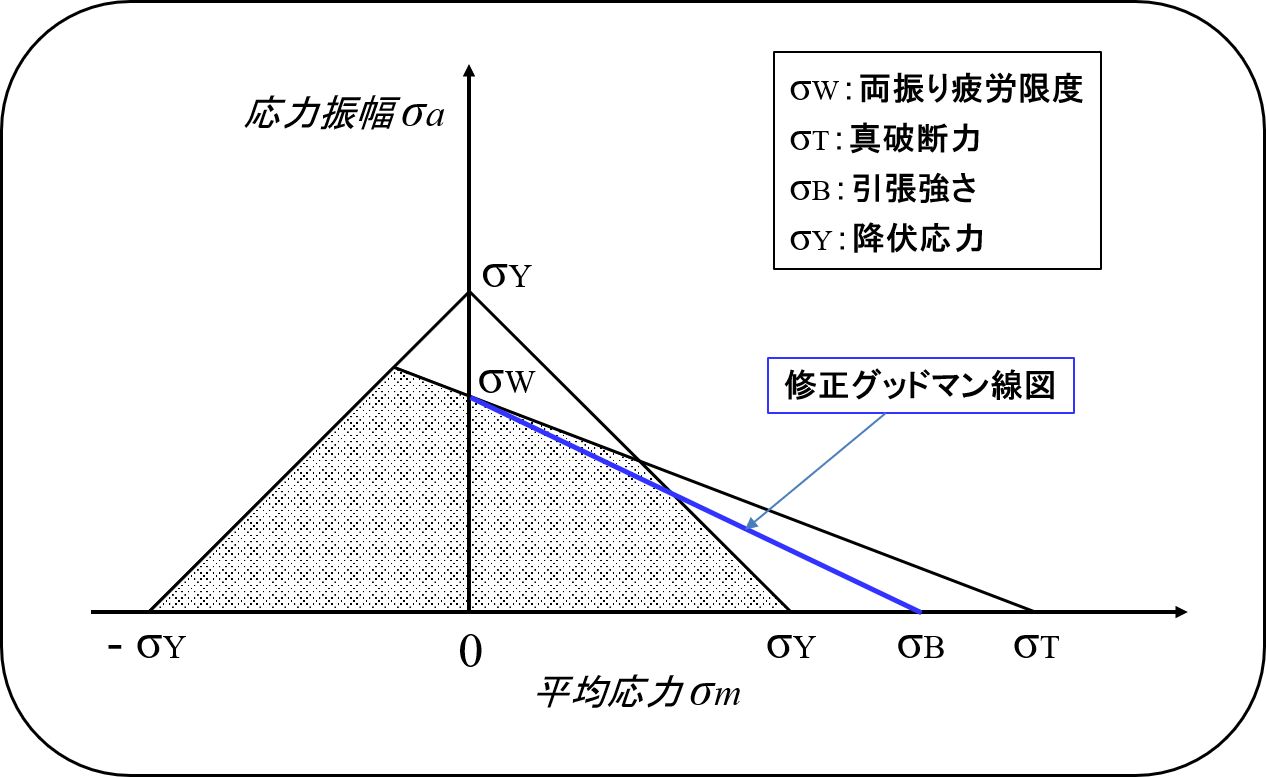
図2 疲労限度線図と修正グッドマン線図
一般的に疲労設計では修正グッドマン線図が利用されることが多いですが、疲労限度が平均応力とともに直線的に減少するのではなくて、緩やかに減少する二次曲線で結んだものとしてゲルバー線図と呼ばれるものがあります。なお、X軸の降伏応力の点とY軸の両振り疲労限度を結んだ線図をゾーダーベルク線図といいますが、あまり利用されません。
各種金属材料の疲労限度線図は多様でありますが、疲労試験機によって両振り疲労限度、片振り疲労限度、引張強さを測定し、この3点を結んだ線図はより正確な疲労限度線図といえます。図3で応力比0として示してある破線は片振り試験の測定点を意味しますが、疲労限度線図との交点が片振り疲労限度の値を示します。
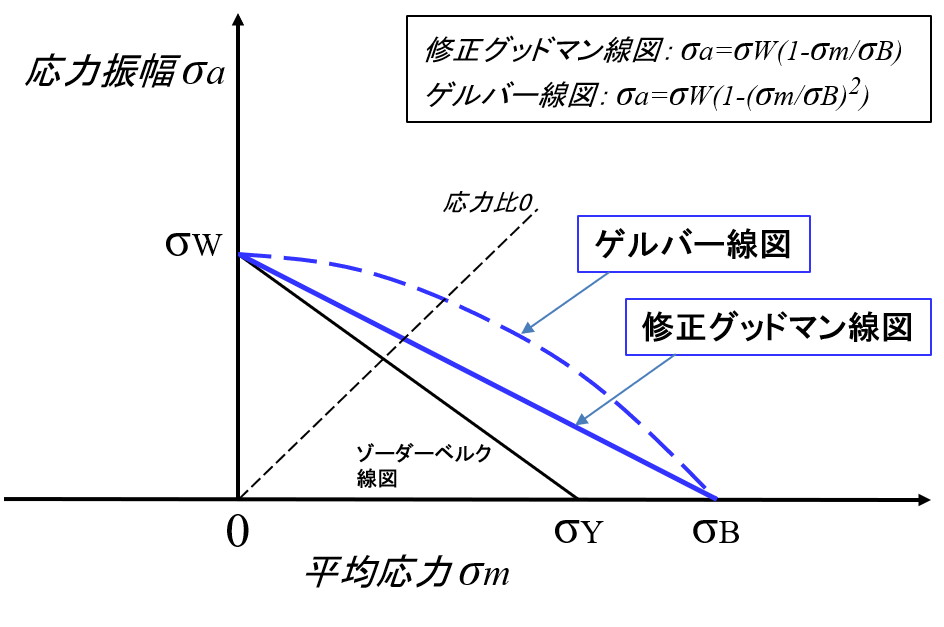
図3 各種疲労限度線図
平均応力の影響
図4にてSUS304ならびにSCM435の引張平均応力に対する引張疲労限度の分布域を表しますと、SUS304ではゲルバー線図付近に分布し、一方SCM435では修正グッドマン線図とゲルバー線図との間に分布します。グラフではX軸、Y軸ともσm/σB(平均応力/引張強さ)とσa/σW(応力振幅/両振り疲労限度)で規格化してあります。いずれの場合でも修正グッドマン線図を用いて設計すればより安全側の設計といえます。
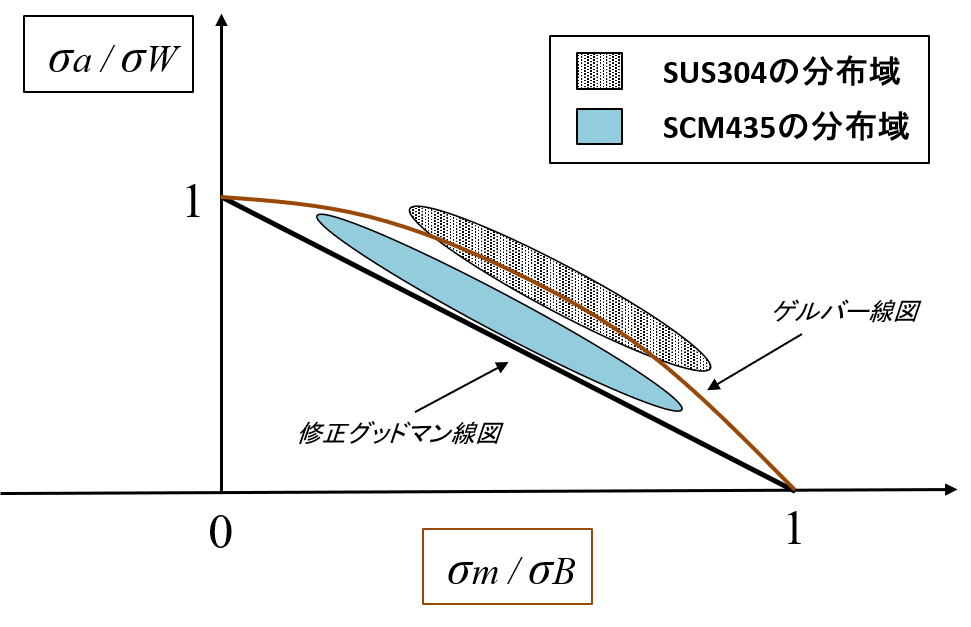
図4 平均応力と疲労限度の関係(各種材料)
次に、切欠き材の場合について説明します。切欠き材の両振り疲労限度は平滑材に比べて切欠き係数で除した値になって低くなります。図5Y軸のσW1とσW2がその位置を表しています。疲労限度は引張平均応力とともに低下していきますが、一般的にはX軸上の点を真破断力とする疲労限度線図で求めます。しかしながらX軸上の点として試験値の入手しやすい引張強さとする修正グッドマン線図で考えても大差はありません。切欠き材についても両振り疲労限度、片振り疲労限度、そして引張強さを用意して各点を結ぶ線図が疲労限度線図として利用しやすいと考えられます。
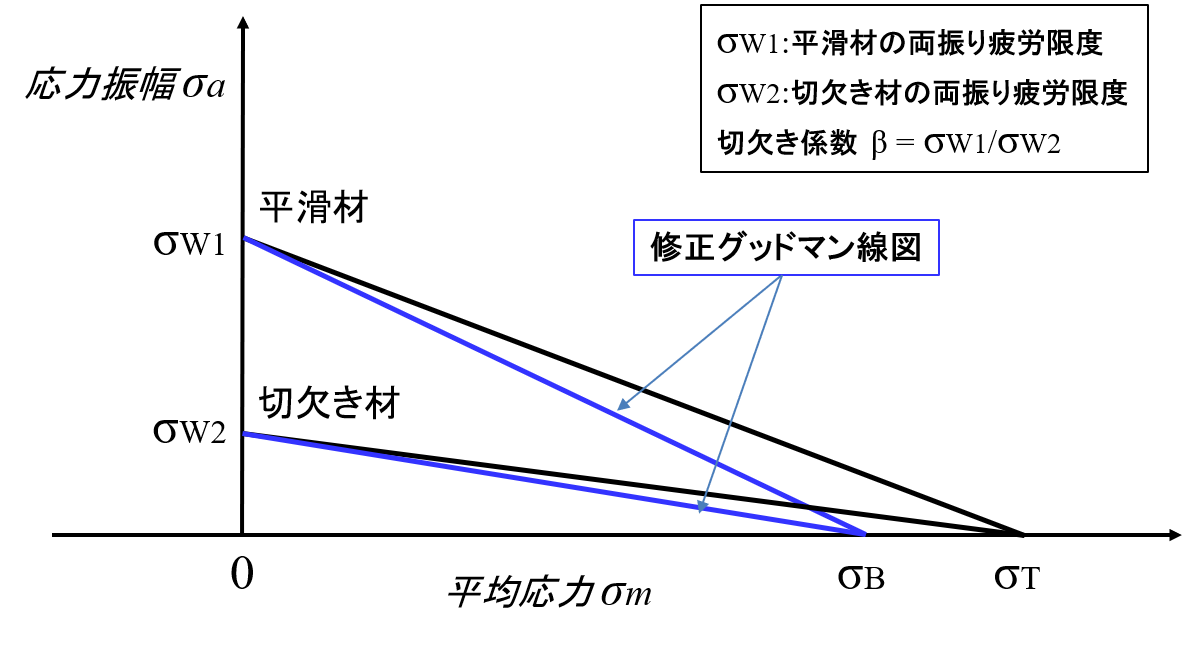
図5 疲労限度線図の関係(平滑材と切欠き材)
なお、曲げ疲労やねじり疲労の疲労限度に及ぼす平均応力の影響は引張圧縮の場合と比べて小さいと言われています。その要因として、疲労の繰返し応力による塑性変形が起こって応力分布が変化し、表面付近の平均応力が初期状態から低下するといった考えがあります。
高強度鋼のケース
引張強さが1500MPaクラス以上の高強度鋼の疲労限度線図について測定例は少ないのが現状ですが、例えば引張強さが2000MPaクラスのマルエージング鋼などの疲労限度線図は図6に示すように特異な形をしています。平均応力が0から増えるにつれて疲労限度は急激に減少し、その後殆ど一定に変化しない分布曲線となることが知られています。この現象の説明として、表面付近に存在する非金属介在物が強い応力集中源となって平均応力が増加するとともに強い応力集中の影響を及ぼして疲労限度が大きく低下し、さらに平均応力が増加して応力集中部の最大応力が降伏応力を超えると疲労限度は平均応力の大きさに関係なくほぼ水平に移行すると考えられています。
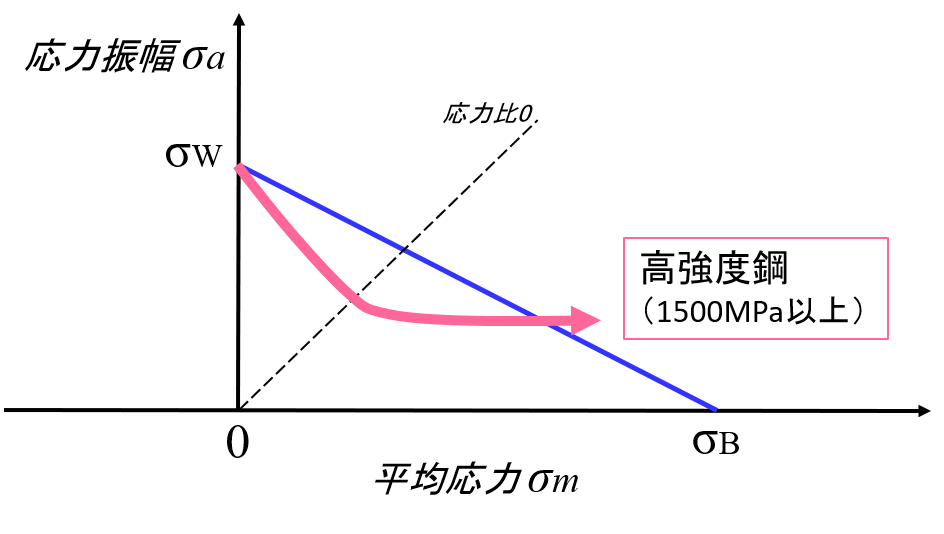
図6 高強度鋼の平均応力と疲労限度
ねじ部品(ボルト)のケース
ねじ部品(ボルト)は過去から長年各種多用なものが大量に使用されている部材であるにもかかわらず、疲労限度線図の測定例は少ない状況です。疲労試験機の導入コスト、長期の試験時間がかかるといったことが要因かも知れません。
現在までのところ、ボルトの疲労限度は平均応力の影響を殆ど受けないと言われています。ボルト単体の疲労限度は一般的に応力比0の条件である片振り試験で測定されます。また、締結体においてもボルトにかかる繰返し応力は最低応力が0以上である部分片振り振動となります。仮に、疲労限度を図7で示しますと以下のようなイメージになると考えられます。
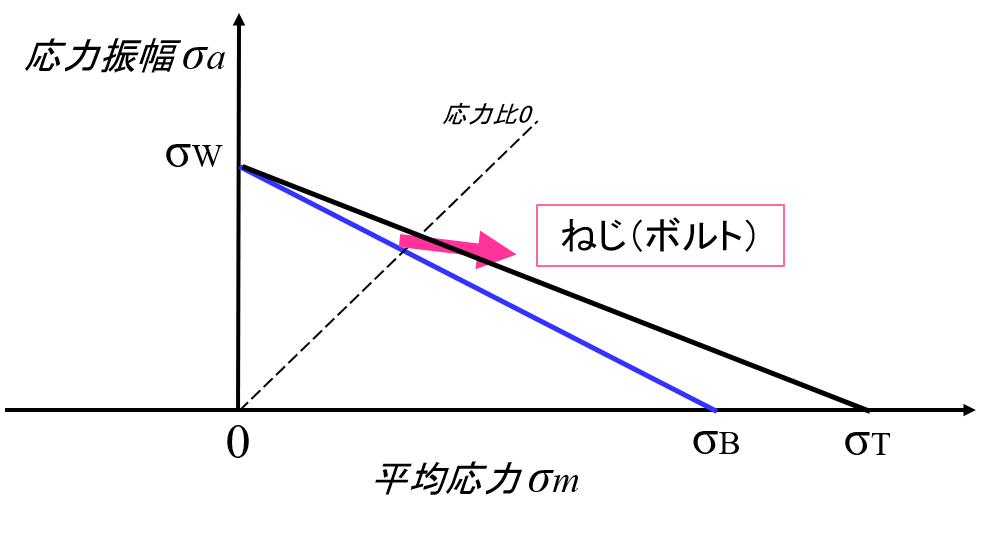
図7 ねじ部品(ボルト)の疲労限度に及ぼす平均応力の推定
近年、特にボルトについて疲労破壊に対する安全・品質問題の解決に向けた取組みが重要になってきています。弊社におきましても、疲労試験機を導入し、各種ねじ部品単体および締結体について疲労試験を実施しております。あわせて、ねじ(ボルト)の疲労限度線図についても詳細を明らかにしていきたいと考えています。
疲労強度に関連する以下のねじ締結技術ナビ技術資料・コンテンツもあわせてご覧ください。





