ボルトの破損の形態
ねじ、ボルトの材料における『破損』は大きく「破損」、「破壊」、「破断」の3つに分けられます。
それぞれの定義は、以下のようになります。
破損
材料の一部が分離するか永久変形を起こすことを破損という。破損は必ずしも使用上の支障を意味するとはかぎらない。
破壊
材料の一部または全体が分離するか著しく大きい永久変形を起こして使用に耐えられなくなることを破壊という。
破断
材料が破壊して分離することを破断という。
上記の定義を踏まえたうえで、まず引張り試験における延性材料と脆性材料の丸棒の挙動を取り上げた後、ボルトの破損形態について触れます。
機械部品に多く用いられる材料は大きく2つに分けられます。
材料を引っ張ったとき「伸び」や「絞り」を伴う延性材料―図.1[文献(2)より]参照―と、「伸び」や「絞り」がほとんど伴わない脆性材料―図.2[文献(2)より]参照―であります。
延性材料である軟鋼の一つにJIS規格の「一般構造用圧延鋼材」のSS400があります。このSS400の丸棒を引っ張った時の応力σとひずみεの関係が図.1[文献(2)より]の線図であります。
荷重が作用し始めてから応力σとひずみεの「比例関係」が成立している区間が―直線部分―「弾性領域」といいます。この「比例関係」は「フックの法則」で知られています。
弾性領域を超えて荷重が加えられると、丸棒内部に「すべり」が生じ、応力は大きく変動しながらひずみも増加します。点Aが「下降伏点」であり、降伏応力σyとします。「すべり」は45°・135°の方向の丸棒表面に「リューダース線」として現れます。
更に荷重をかけても応力はそれほど増加せず、ひずみがかなり増加します。この領域が主に丸棒が伸びる「加工硬化」の領域です。応力は最高点Bに達した後、やや減少しつつ点Cで破断します。点B以降では「くびれ」が生じ、破断面は「塑性変形」の証である「カップコーン型」を示します。なお点Bの応力が丸棒の「引張り強さ」、点Cの応力が「破断応力」となります。
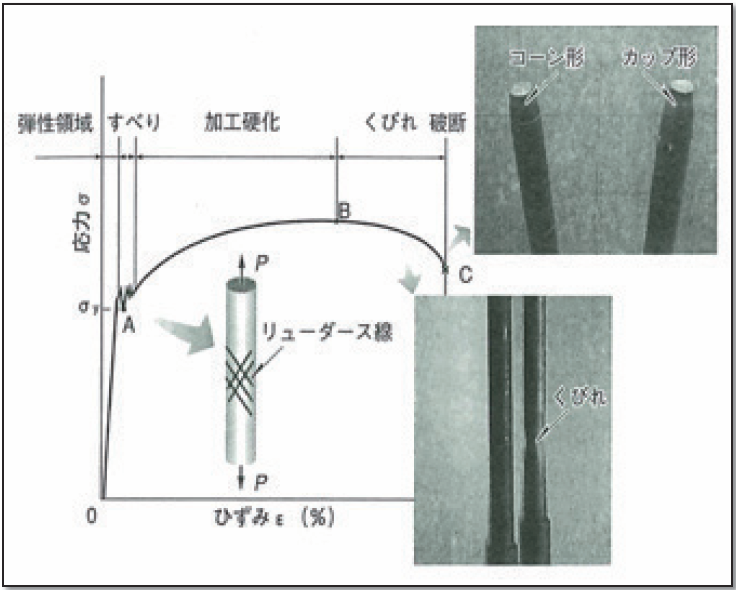
図.1 延性材料の破断形状と応力-ひずみ線図
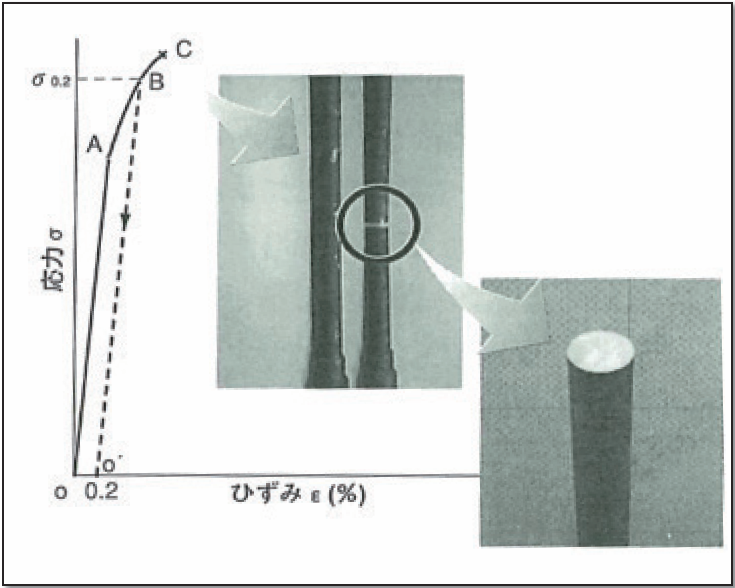
図.2 脆性材料の破断形状と応力-ひずみ線図
焼き入れた高炭素鋼のような脆性材料を引っ張ると、図.2[文献(2)より]のような応力-ひずみ線図を描きます。両者の関係はしばらく荷重(応力)の増加に伴い線形を示します。
ところが点Aを越えると非線形になり、やがて破断(点C)します。非線形領域突入後のある点から除荷すると、負荷時の直線にほぼ平行に点0’に戻り、00’に相当する「残留ひずみ」が残ります。その大きさが0.2%になる点Bの応力が「耐力」であり、通常σ0.2と表記されます。
では、次にボルトの破損形態について述べます。写真.1と写真.2は延性材料SS400強度区分4.8と脆性材料SCM435強度区分10.9のボルトを引張り試験でそれぞれ破断させたものです。SS400及びSCM435のボルトの破断面は、45°もしくは135°に傾いており、2つの試験片共に同様の破断の形態をしていることがいえます。
引張り荷重によるボルトの破断の発生個所は、ねじ谷底であります。これはボルトのねじ谷底の応力集中係数によるものです。ボルトの応力集中係数αは、断面の平均応力σnom、最大応力σmaxとおくと、
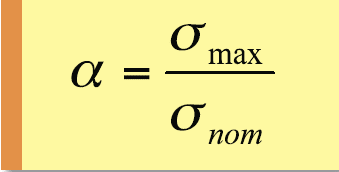
と表され、ボルトの場合はα=3~4と知られています。つまり、ボルトの破損/破断はボルトの表面、特に応力集中の高いねじ谷底から発生します。このようなボルト・ナットの引張り荷重による破断については、沢俊行「再入門・材料力学」に次のようにあります。


写真.1 M20 4.8 延性破壊 試験片と破断面

写真.2 M12 10.9 脆性破壊 試験片と破断面

写真.3 M12 4.8 試験片と破断面
写真.3は、ボルトが破断するまで締付けトルクTを加えたものです。破断箇所は写真.3にあるように、ナット座面側第1ねじ谷底で締付け状態において最も応力が高くなる個所と知られている部分です。また、破断面も引張り試験によるものとは明らかに異なり、平坦でねじ切られた状態が見て取れます。

写真.4 M12 4.8 疲労破壊 試験片と破断面
写真.4は、疲労破壊したボルトです。疲労破壊の破断面の特徴は、写真.3の破壊トルクによる破断面よりも更に平坦であり、まるで刃物で切ったように滑らかな点である点にあります。
参考文献
1 山本 晃(1985) 『ねじ締結の理論と計算』 養賢堂
2 沢 俊行(2007) 『再入門 材料力学 基礎編』p.28~31 、p.46日経BP社





