(この技術資料のダウンロードはこちらから)
応力拡大係数とは
応力拡大係数は、き裂や欠陥が存在する材料の強度評価に用いられる最も重要なパラメータです。今、最も単純な例として、無限遠の平板中に長さ2aの鋭い貫通き裂がある材料を、一軸方向(Y方向に)に応力σで引張った際に、き裂近傍の弾性応力状態は図1のように表されます。式中のKが応力拡大係数と呼ばれ、図中赤色で示した式で求められます。式中のαは材料とき裂の形状、応力の負荷形式などで決まる定数で、種々の条件下についてこの定数が計算されており、例えば無限板中の貫通き裂ではαは1です。き裂長さが長くなるにつれて応力拡大係数は増加し、き裂前方の応力も増加します。aとαが異なる材料同士であっても応力拡大係数Kが同じ値であれば両材料はき裂先端近傍の応力分布が等しくなります。この特性を活かして、実機材の破壊現象を小型試験材の破壊力学的な検証で実現できることが可能になります。
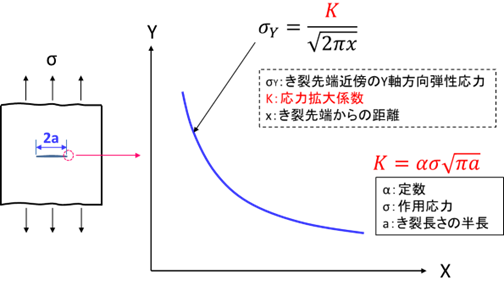
図1 き裂先端近傍の弾性応力分布
応力拡大係数(範囲)と疲労寿命との関係(パリス則)
疲労き裂に繰返し荷重が加わると応力の変動に伴ってK値も変動します。このため、疲労き裂を進展させる力学的パラメータは応力拡大係数Kではなくて応力拡大係数範囲ΔKと呼ばれる変動幅になります。ΔKはKの変動範囲で、繰返し応力が最大の時であるKの最大値と繰返し応力が最小の時であるKの最小値の差です。
多くの実験データから疲労き裂進展速度da/dnと応力拡大係数範囲ΔKの間に次式で示される関係が成立することが知られています。
da/dn = C(ΔK)^m
ここで、aはき裂長さ、nは応力の繰返し数、Cとmは実験定数でm=2-8程度になることが多いと言われています。da/dnは繰返し数1回あたりのき裂進展量を意味します。図2は疲労き裂進展速度da/dnと応力拡大係数範囲ΔKの関係を模式的に示した図です。da/dn-ΔK関係図は一般的に両対数で表示され、この関係図は第IIa段階、第IIb段階、第IIc段階に区別されます。第IIbにおいてき裂が安定して進展し、上記の関係式(パリス則と呼ばれています)が成立して勾配mの直線になります。
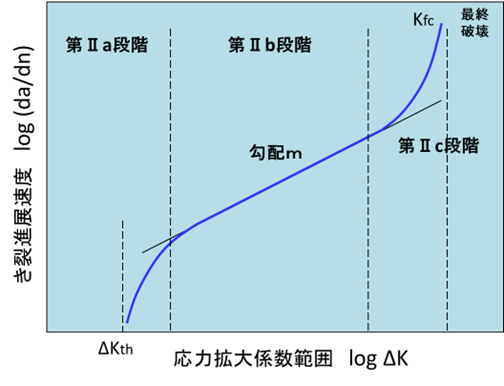
図2 疲労き裂進展速度と応力拡大係数範囲の関係図
応力拡大係数と疲労寿命について、詳しくは、ねじ締結技術ナビ技術資料の「疲労き裂と応力拡大係数」をご覧ください。
また、疲労強度に関連する以下のねじ締結技術ナビ技術資料・コンテンツもあわせてご覧ください。




.png)

