ねじの締付けにおいて、ボルトに軸力が発生している状態でナットにトルクを加えて回転させるとき、ボルト軸力とナットに加えるトルクとの関係は、「斜面の原理」の応用として導かれます。
締付けトルクTと軸力Fの関係は、トルク係数K、ボルトの呼び径をdとして、
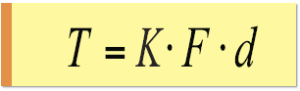
の関係にあります。
ここで締付けトルクTの定義は、
「締付けにおいて、ナット又はボルトの頭部に作用させるトルク」としています。
ねじ締結体の構造上、目標軸力を得るための締付けトルクTは、ナットを固定して
ボルトに締付けトルクTを加えても、またその逆にボルトを固定してナットに締付
けトルクTを加えても結果は同様の軸力を得られるということになります。
ボルトとナットはリード角βの角度で螺旋状にねじ山が切られていますが、ねじ締
結体において締付けトルクTと軸力Fの関係は、ボルトかナットのどちらかのねじ
山を斜面、他方を荷物と見立てて(図1.参照)、斜面を荷物を押して進む場合の力
の作用からよく説明されます。
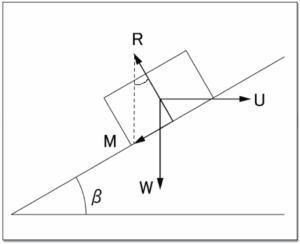
図1.斜面を上がる場合の力の作用
斜面上で荷物を水平方向に押す力をU、荷物の重さをW、反力をR、摩擦力をM、
摩擦角をρ、荷物と斜面の間の摩擦係数をμ、傾斜角をβとします。
斜面上で荷物の進行を妨げる方向に作用する摩擦力Mは、

となります。
ねじを締める場合、斜面に対し荷物を上げることと考えられますので、
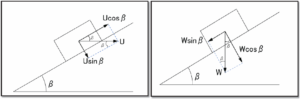
図2.水平方向に押す力Uの分解 図3.重力(荷物の重さW)の分解
図2.図3.に示すように、水平に押す力Uと重力Wを斜面の水平方向と垂直方向に
それぞれ分解し、力のつり合いを求めると、
・斜面水平方向の力のつり合い Ucosβ=Wsinβ+M
・斜面垂直方向の力のつり合い R=Usinβ+Wcosβ となるので、
荷物を水平方向に押す力Uを求めるには、
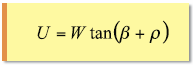
が導き出されます。
また、斜面に対し荷物を下る場合には、摩擦力の向きが逆になることから、

が求められます。
斜面を上がる場合の摩擦力Mは、
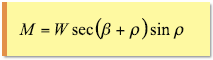
斜面を下る場合の摩擦力Mは、
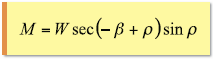
で求められます。





