変動応力について
実機部材の金属疲労現象では、その実働負荷荷重の応力波形が一定応力振幅の繰返しではなくて時間とともに応力波形が変化する変動応力になります。機械構造物などでは緩やかな振動によって発生する比較的大きな応力の上に微小振動による繰返し速度の速い応力が重なる波形、あるいは複数の応力振幅の波形が繰り返される波形などが多く見受けられます。
このような変動応力における金属疲労現象に対して、変動応力波形の計測の問題、および変動応力が疲労に及ぼす影響の問題の両者について過去から検討が行われてきています。ここではこの変動応力下の金属疲労について変動応力波形の計測、および変動応力が疲労に及ぼす影響について簡単に紹介します。
変動応力波形の計測
S-N曲線を用いた疲労寿命設計では実機部材に作用する応力値を求める応力評価が重要であります。負荷応力が変動する場合、この変動応力波形を計測する方法として、時間とともに変化する応力値の頻度を求める必要があり、応力頻度読み取り法といいます。
応力頻度読み取り法はいくつかの方法がありますが、疲労が繰返し応力によって発生すること、平均応力の大きさにも影響されること、大きな応力変動に伴う塑性ひずみ幅が疲労損傷に影響することなどが考慮されています。
代表的な応力頻度読み取り法を表1に示します。主な方法として、ピーク法、レンジ法、レンジ・ミーン法、レンジペア法、レインフロー法、レンジペア・ミーン法、全波法があげられます。応力波の特性は、ピークの大きさであるピーク値、応力範囲の大きさである振幅値、応力範囲の中間の大きさである平均値(平均応力)、波動のうねりに相当する大きな応力の変化があります。各種の応力頻度読み取り法は、特に対象とする応力波特性の違いで特徴付けされています。
表1 代表的な応力頻度読み取り法
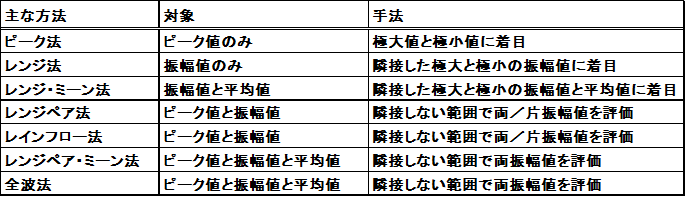
図1に(a) ピーク法と(b) レンジ法の概念図を示します。
ピーク法は、応力波形の山である極大値と谷である極小値のみを対象とし、各ピーク波形について図1 (a)の枠図に示したような破線部分があるかのように仮定して読み取る方法です。図1 (a)の例では例えば図中P6もカウントすることになりますが、P6の部分は実際の疲労過程では影響が小さいですがピーク法によるカウントでは過大に評価することになります。一般的にピーク法は実際より過大に評価する方法といわれており、より安全側の寿命推定を与えることになります。
レンジ法は、隣同士の応力波形のレンジ(応力範囲)を対象として図1 (b)のように各波形の応力範囲σiを順次読み取る方法です。応力範囲の半分がS-N曲線でいわれる応力振幅に該当しますが、大きな波に小さな波が重なった場合などでは大きな波のレンジを数えずに最大応力のカウントを逃したりします。一般的にレンジ法は実際より過小に評価する方法といわれており、より危険側の寿命推定を与える懸念があります。なお、レンジ法で各応力範囲の中間点の応力を平均応力として読み込む方法がレンジ・ミーン法になります。
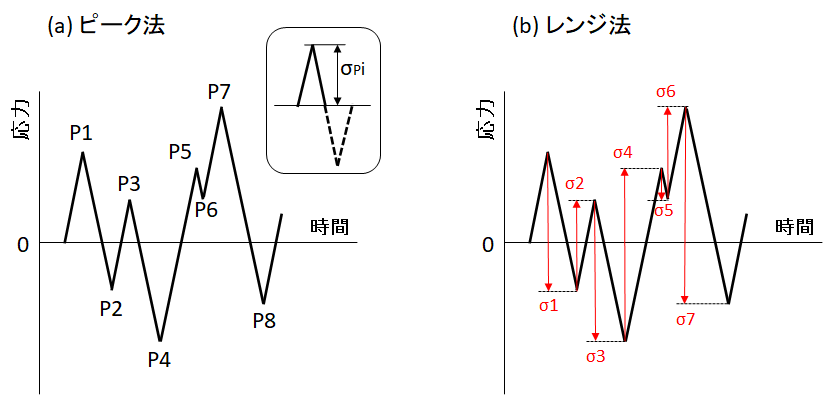
図1 (a) ピーク法と(b) レンジ法の概念図
図2に(c) レンジペア法と(d) レインフロー法の概念図を示します。
レンジペア法は、応力の上昇過程と下降過程において等しいレンジ(応力範囲)のペア(図2 (c)の網掛け部分)を作成し、これを順次抜き出して計数し、最後に残った大きなレンジのペア(図2 (c)の1から8までの大きな応力範囲、および8から15までの大きな応力範囲)を数える方法です。材料の応力・ひずみ挙動との対応性がよく、一般的に疲労損傷評価のための応力頻度の計数法として適している方法と考えられています。なお、レンジペア法で各応力範囲の中間点の応力を平均応力として読み込む方法がレンジペア・ミーン法になります。
レインフロー法は、応力の変化を表す時間軸を縦方向に取り、応力波形の変化を屋根に見立てて以下の条件で屋根上を流れる雨の流路をもってレンジ(応力範囲)を計数する方法です。すなわち、
・雨は各屋根の付け根(図2 (d)において番号の振ってある箇所)から順次流れ始める。
・ある最初の屋根先から雨が落ちる時、順次接する各屋根の付け根が最初の付け根より流れ方向側にある限り流れ続け、そうでない場合(最初の出発点より反対寄りの場合)は流れを停止する。
・屋根上の流れは、上層側の屋根から落ちる流れにぶつかると停止する。
そして、順次雨水が流れた横方向の長さを半サイクル分の振幅値(全振幅)として計測します・レインフロー法はレンジペア法をもとにコンピュータ処理を容易にするために考案されたアルゴリズムで、長時間の変動応力波形に対する計数結果はレンジペア法に基本的に一致します。なお、レインフロー法でも平均応力を考慮したプログラム化も容易です。
全波法は、個々の波について平均応力を有する一つの完全波(平均応力を中心にして極大値の波と極小値の波を有するペアの波)として取り出す作業を順次繰返し、各波についてピークの大きさ、振幅値、平均応力を読み取る手法です。
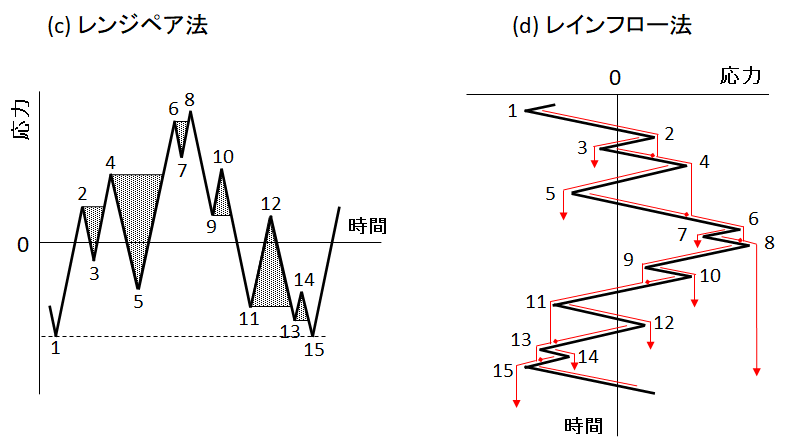
図2 (c) レンジペア法と(d) レインフロー法の概念図
最近ではコンピュータの発達によって種々の読み取り法についてソフトウェアが用意(市販)されており、リアルタイムで処理できるようになっています。変動応力波形によってはどの読み取り法を使っても大差がでない場合もありますが、特に周波数帯域が広く異なる変動波形では差が大きく出ます。一般的にレンジペア法とレインフロー法は周波数帯域による制限がないことから推奨される計測法といわれています。
変動応力と疲労
通常の疲労試験では一定応力の繰返しでS-N曲線を求めることが多いですが、実機では複雑な応力波形が繰返し発生します。このような複雑な応力波形を受ける部材の疲労寿命の検証には実働荷重による疲労損傷の知見が必要になりますが、疲労試験を実働荷重の応力波形で実施することは至難の業ともいえます。一般的には実働応力をモデル化した幾つかの応力波形によって試験されています。
変動応力による疲労試験
機械構造物では周波数の低い大きな応力波形に周波数の高い小さな繰返し応力波形が重なる重畳波が多く観察されます。図3に重畳波形の例を示しました。特に車両用台車枠やばねなどで観察される波形をモデル化したものとして位置づけされたりします。
重畳波では低周波の大きな応力振幅と高周波の小さな応力振幅の両者の累積損傷を考えますが、双方の応力による相互干渉についても考慮することが重要です。重畳波の疲労試験から、応力振幅σ1のみの場合の疲労強度は応力振幅σ2が存在し始めると低下すること、すなわち小さな応力振幅が疲労限度以下であっても疲労寿命に大きく影響を及ぼすことが確かめられています。
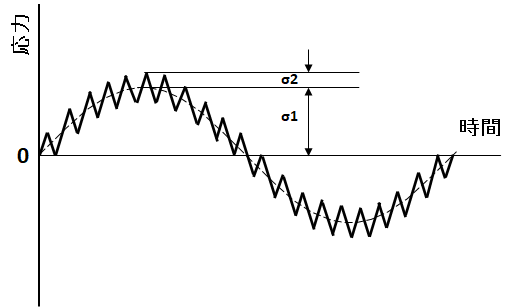
図3 疲労試験で行う重畳波形の例
図4にいくつかの応力振幅が繰り返される変動応力振幅波形を示しました。この変動応力振幅波形では疲労限度以上の波形と疲労限度以下の波形が混在しており、この過小応力は実機の応力頻度の観察結果を基に非常に多く繰り返したりします。応力の大小の順序や繰り返し数の分布も任意に設定できますが、二つの応力レベルが繰り返される二段多重応力波形の実験が比較的数多く行われています。
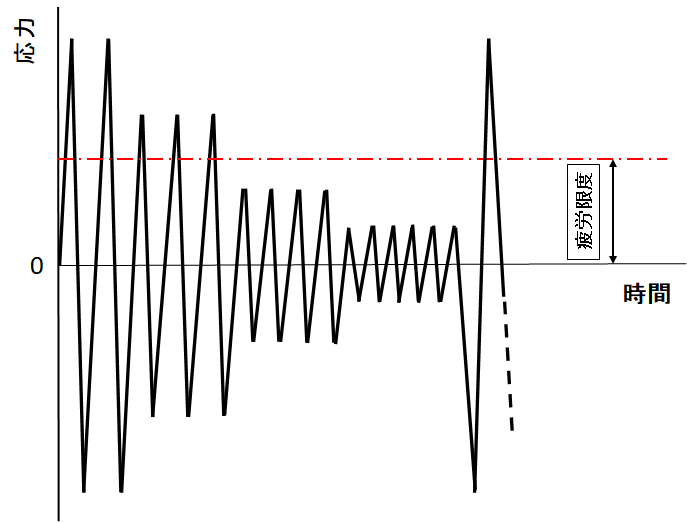
図4 疲労試験で行う変動応力振幅波形の例
線形累積損傷則との関係
S-N曲線における疲労限度は一定の応力振幅の繰返し条件で求められます。変動応力の繰返しによる疲労破壊ではすべての応力成分が疲労限度以下の場合に疲労破壊が生じるかどうかは不明な点がありますが、一般的には疲労限度以下の応力振幅のみの変動応力下では疲労破壊が発生しないという考えが支配的です。しかし、少数回でも疲労限度以上の過大応力が作用すると、疲労限度以下の応力でも疲労損傷が進行すると考えられています(メカニズム的には固着転位の解放が挙げられます)。すなわち、疲労限度以上の応力振幅と疲労限度以下の応力振幅が組み合わさる場合は、疲労限度以下の応力振幅も考慮した寿命推定が必須です。
過小応力を含む変動応力振幅波形による疲労試験から、疲労限度以上の応力振幅のみを扱う線形累積損傷則(マイナー則)では大きくずれることが明らかになっています。疲労限度以下の過小応力が疲労損傷の累積に大きくかかわっており、S-N曲線の傾斜部を直線で疲労限度以下まで延長した新しいS-N曲線で線形累積損傷則を適用する修正マイナー則が実機の寿命推定でよく使用されます(図5)。
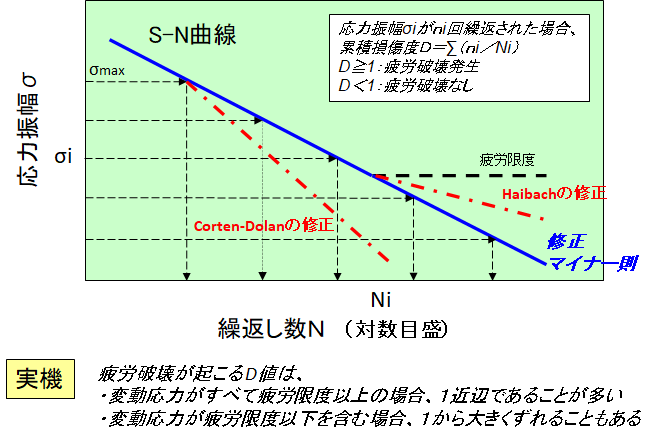
図5 修正マイナー則による累積損傷度
線形累積損傷則で変動応力がすべて疲労限度以上の場合は特殊な場合を除いて1近辺であることが多いといわれます。一方、変動応力が疲労限度以下の過小応力を含む場合は修正マイナー則でも1から大きくずれることがあり、安全設計上1以下になる条件が重要な判断材料になりますが、現在のところ1以下になる明確な条件はわかっていません。そのため、現物の実機波形を模した疲労試験を行わない場合は懸念が残りますが、安全率を見込んでD値を0.3程度と見積もる考え方もあります。
線形累積損傷則を修正した他の修正線図としてCorten-Dolanの方法およびHaibachの方法があります。前者はS-N曲線における傾斜部で応力頻度の最大応力の点から低寿命側に直線を延長したもので、低応力側の疲労損傷を大きく考えたものです。後者はS-N曲線における傾斜部と疲労限度との交点から延長する直線の傾斜を緩やかにしたもので、過小応力の影響を長寿命側に設定しています。疲労限度以下の応力頻度が疲労限度以上の頻度に比較して極端に多い場合にはHaibachの修正法が適切といわれています。
疲労強度に関連する以下のねじ締結技術ナビ技術資料・コンテンツもあわせてご覧ください。





